命題36
もし、単位から始まる任意個の数が連続して2倍に比例し、全ての和が素数になるまで定められ、最後をその和にかけられてある数を作るならば、その積は完全数である。

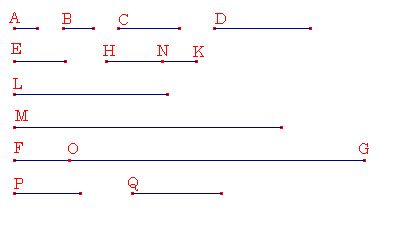
単位から始まる任意個の数ABCDが2倍に比例し、全ての和が素数になるまで定められ、また、Eがその和に等しく、EにDをかけられてFGを作るとせよ。
FGが完全数であると主張する。
ABCDが個数の上でいくつになってもEから始まり2倍に比例になる同じ個数のE、HK、L、Mをとるとせよ。
それゆえに、等間隔比によりAはDに対して、EはMに対する。propositionⅦ14
それゆえに、EとDの積は、AとMの積と等しい。propositionⅦ19
また、EとDの積はFGである。
それゆえに、AとMの積もまたFGである。
それゆえに、AはMをかけられてFGを作る。
それゆえに、MはFGを割り切って、その商はAの中の単位である。
また、Aは2である。
それゆえに、FGはMの2倍である。
しかし、M、L、HK、Eは連続して他のそれぞれの2倍である。
それゆえに、E、HK、L、M、FGは2倍に比例で連続して比例している。
第2のHKと最後のFGからそれぞれ最初のEに等しいHNとFOが引かれたとせよ。
それゆえに、第2が第1に対する超過は第1に対して、最後が第1に対する超過は最後の前までの和に対する。propositionⅨ35
それゆえに、NKはEに対して、OGはM、L、KH、Eの和に対する。
そして、NKはEに等しい。
それゆえに、OGはM、L、KH、Eの和に等しい。
しかし、FOもまたEに等しい。
そして、EはABCDと単位の和に等しい。
それゆえに、FG全体は、E、HK、L、M、ABCDと単位の和に等しく、それは、それらによって割り切られる。
FGはまた、ABCD、E、HK、L、Mと単位を除いて、他の任意の数によって割り切られないと主張する。
もし可能ならば、ある数PがFGを割り切り、PをABCD、E、HK、L、Mのどの数とも同じでないとせよ。
PがFGを割り切った商と同じだけQの中に単位があるとし、それゆえに、QはPをかけられてFGを作る。
しかし、加えてEはDをかけられてFGを作る。
それゆえに、EはQに対して、PはDに対する。propositionⅦ19
そして、A、B、C、Dは単位から始まり連続して比例するので、それゆえに、DはA、B、Cを除いて、他の任意の数によって割り切られない。propositionⅨ13
そして、仮定よりPはA、B、Cのどの数とも同じでない。
それゆえに、PはDを割り切らない。definitionⅦ20
しかし、PはDに対して、EはQに対する。
それゆえに、EはまたQを割り切らない。
そして、Eは素数であり、そして、任意の素数はそれが割り切らない全ての数は素である。
それゆえに、EとQは互いに素である。propositionⅦ29
しかし、素は最小で、最小の数は同じ比をもつ数を割り切り、商が同じで、前項は前項を、後項は後項を割り切り、EはQに対して、PはDに対する。propositionⅦ21、propositionⅦ20
それゆえに、EはPを割り切り、その商はQがDを割り切ったものと同じである。
しかし、DはA、B、Cを除いて、他の任意の数によって割り切られない。
それゆえに、QはABCの1つと同じである。
それをBと同じであるとせよ。
B、C、Dは個数の上でいくつになってもEから始まって同じ個数のE、HK、Lをとるとせよ。
E、HK、LはB、C、Dと同じ比である。
それゆえに、等間隔比によりBはDに対して、EはLに対する。propositionⅦ14
それゆえに、BとLの積は、DとEの積と等しい。
しかし、DとEの積はQとPの積と等しい。
それゆえに、QとPの積はまたBとLの積と等しい。propositionⅦ19
それゆえに、QはBに対して、LはPに対する。
そして、QはBに等しい。
それゆえに、LはまたPに等しく、これは不可能である。propositionⅦ19
これはPは定められた数のどれとも等しくないからである。
それゆえに、FGをA、B、C、D、E、HK、L、Mと単位を除いて割り切る数はない。
そして、FGは、A、B、C、D、 E、HK、L、Mと単位の和であることは証明されていた。
そして、完全数はその約数の和と等しい。
それゆえに、FGは完全数である。definitionⅦ22
それゆえに、もし、単位から始まる任意個の数が連続して2倍に比例し、全ての和が素数になるまで定められ、最後をその和にかけられてある数を作るならば、その積は完全数である。